Pisagor Bağıntısı ve Pisagor Teoreminin İspatı
Pisagor adındaki bir matematikçi, M.Ö 500’lü yıllarda inanılmaz bir şey keşfetmiştir ve adına pisagor bağıntısı denmiştir. Bulduğu şey, bugün dik üçgen kavramının geçtiği her yerde karşımıza çıkar ve bir çoğumuz bunu anlamakta zorlanırız. Aşağıda, pisagor teoremi ile ilgili olarak basit seviyeden karmaşık seviyeye doğru bir anlatım yapmaya çalıştım.
Pisagor Bağıntısı Nedir?
Bilindiği üzere, bir açısı 90 derece (Dik Açı) olan üçgenlere “Dik üçgen” adı verilmiş. 90 derecenin karşısındaki kenara “Hipotenüs”, diğer iki kenara ise “dik kenar” adı verilmiş. Şimdi gelelim pisagorun bu dik üçgen ile ilgili bağıntısına;
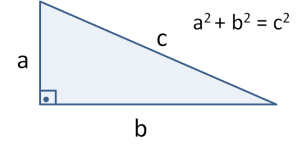
Pisagor bağıntısı derki: “Bir dik üçgen’de; Hipotenüs’ün uzunluğunun karesi , diğer iki dik kenarın karelerinin toplamına eşittir”. Aşağıdaki şekle göre; a2 + b2 = c2 ‘dir.
Temel seviye için bu kadar bilgi yeter sanırım, Teoremin nasıl oluşturulduğu ve daha ileri seviye bilgileri, başlangıç seviyesi sorularından sonra okuyabilirsiniz.
Buraya kadar yazdıklarımızın kısa bir özetine bakarsak;
- Dik üçgenlerin 1 açısı 90 derecedir
- 90 derecenin karşısındaki kenar hipotenüs’tür
- Diğer 2 kenara dik kenar denir
- Hipotenüs dik üçgenin en uzun kenarıdır
- a2 + b2 = c2
Pisagor Bağıntısı için örnek sorular;
Sorular içinde kolaylık olması açısından, temel bir kaç kuralı vermekte fayda olabilir. Pisagor bağıntısında yola çıkarak ( hesaplamalar sonucu ), bazı standart dik üçgen tiplerinden bahsedebiliriz. Bunları bilmek soruları çözerken bize hız kazandırır. Hemen bu üçgenlerden bahsedip, soruları çözerken nasıl faydalanacağımızı görelim. Aşağıdaki pisagor örneklerini inceledikten sonra “Ücretsiz Geometri soru bankası PDF” istersen buraya tıklayarak indirebilrsin.
- 3, 4 ,5 dik üçgeni
- 5, 12, 13 dik üçgeni
- 8, 15, 17 dik üçgeni
- 7, 24, 25 dik üçgeni
Yukarıda kenar uzunlukları verilen üçgenler daima dik üçgendir. Formülümüzü uyguladığımızda her biri için denklik sağlanmış olur.
- a2 + b2 = c2 –> 32 + 42 = 52 –> 25=25
- a2 + b2 = c2 –> 52 + 122 = 132 –> 169=169
- a2 + b2 = c2 –> 82 + 152 = 172 –> 289=289
Şimdi sorularımıza geçelim,
Soru1:
 a2 + b2 = c2
a2 + b2 = c2
52 + 122 = c2
25 + 144 = c2
169 = c2
√169 = √c2
13 = c
Soru2
a2 + b2 = c2
ABD dik üçgeninde;
32 + 42 = c2
5 = c –> |AD| = 5
|AD| = |DC| –> |DC|= 5
|BD| + |DC| = |BC|
4 + 5 = |BC|
|BC| = 9 cm
ABC dik üçgeninde;
32 + 92 = c2
90 = c2
√90 = √c2
3√10 = c2
Soru3:
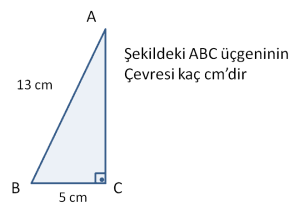
Aşağıdaki şekildeki üçgen tipik bir 5, 12, 13 dik üçgenidir. Bu nedenle herhangi bir hesapla yapmadan, |AC| uzunluğunun 12 cm olduğunu söyleyebiliriz. Bu durumda ABC üçgeninin çevresi 30 cm’dir.
Pisagor Bağıntısının Açıklaması
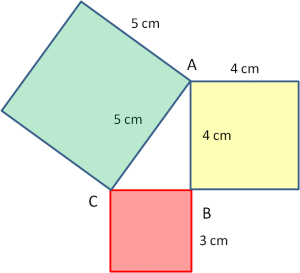
Formülünü yukarıda verdiğim bu teoremi aşağıdaki şekil üzerinde açıklayabiliriz. Pisagor bağıntısının ispatı için aşağıdaki şekilde görüldüğü gibi, ABC dik üçgenin her bir kenar uzunluğunu kullanarak birer tane kare çizelim. Karelerin alanları arasındaki ilişki pisagor bağıntısının keşif sebebidir. Buna göre, hipotenüs kenarının oluşturduğu karenin alanı, diğer iki kenarın oluşturduğu karelerin alanlarının toplamına eşittir. Pisagor bağıntısı sorularını çözerek kendini geliştirebilirsin.
25 = 16 + 9
25 = 25
Aşağıdaki şekilde ise bu teoremin çizimsel olarak gösterimi mevcuttur.
Pisagor Kimdir?
Pisagor orjinal adıyla Phythagoras yazının başında belirttiğim gibi M.Ö 500’lü yıllarda yaşamıştır. Kendisi İyonyalı olup, Pisagorculuk akımının babasıdır. Hakkında fazla kaynak bulunmadığı için bilgilerimizi öğrencilerinin kuşaktan kuşağa anlattıkları ile sınırlıdır. Sadece “Pisagorculuk” akımının babası sıfatlarıyla anılmaz. Aynı zamanda kendisine “Sayıların babası” ve “Bilgeliğin Dostu” sıfatları da verilmiştir.
Yaşadığı dönemde matematik konusunda öncü ve lider kabul edilen ülke Mısır’dır. Dolayısı ile eğitmeni ve öğretmeni Tales’in isteğiyle kendini geliştirmek için Mısır’a gitmiştir. Günümüzde de kullanılan teoremin yaratıcısı pisagor Mısır’da hedefine ulaşmış, kendini geliştirmiştir.
Pisagor’un kendisi ve öğrencileri matematiğin üstünlüğüne inanmışlardır, onlara göre gerçekleşen her şey matematik sayesinde tespit edilebilir ve ölçülebilir. Tales’in öğrencisidir, ortaya attığı “pisagor teoremi” ya da “pisagor bağıntısı” matematiğin babası olduğunu kanıtlar niteliktedir.

Pisagor
Pisagor Teoremi Videolu Anlatım
Resimli anlatımlarım yeterli gelmediyse Youtube üzerinde “Şenol hocanın pisagor bağıntısı” ya da “tonguç akademinin pisagor bağıntısı” videolarını izleyebilirsin. Pisagor bağıntısı ve çok daha fazlası için ücretsiz soru bankasına buradan ulaşabilirsin.
Benzer Konular:



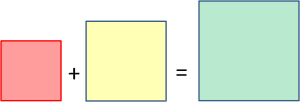

performans ödevim için lazımdı işime yaradı çok teşekür edeim
Pisagor teoremini en kolay anlaşılır biçimde yazmışsınız.
çok güzel işime yaradı
çok teşekkür ederim çok güzel bir ödev yaptım
çok güzel bir site ödevimi tamamlamam çok iyi oldu
zaten pisagor bağıntısı basit.lütfen diğer yani zor
konuları da açıklayın
Anlatılmasını istediğiniz diğer konu başlıklarını verebilirseniz, ilgili konu başlıklarına ait çalışma yapabilirim.
8. sınıf konuları hiç işime yaramadı cenk ama olsun saol birazdaha zor olsaydı daha iyi olurduu…
saolasın yazılıma fayda eder inşallah
yardımcı oldugunuz için tşk ederim ben deniz yaren